This is a continuation of my previous post on implementing a generic A/B testing service – here I will discuss the intricacies around one of the biggest problems faced: the problem of supporting multiple simultaneous experiments, some of which may influence the outcomes of others. The solution discussed here is based on Google’s approach to A/B testing.
Allowing a user to be in more than one experiment
One of the first issues to address is when it is acceptable for a user to be in two experiments at once. Of course, if we have several experiments testing the same thing (e.g. in the advertisement use-case, where there are several statistical models and we want to find out which one yields the highest click-through rate), then any given user can only be in one of those experiments. On the other hand, if we have two unrelated experiments which are testing completely independent features, then it’s fine for a user to be in both experiments at the same time.
We need a way to define and represent experiments in a way that would enable us to capture the different semantics between similar and independent experiments. For this, we borrow Google‘s terminology:
- Layer – A layer represents a specific type of A/B test. For example, we may have a layer for
representing the A/B testing of statistical models used for boosting click-through rates. - Experiment – An experiment lives within a parent layer and each experiment represents a specific test. For example, we may have an experiment for
testing model #5.
These terms are depicted more clearly in the diagram below, which shows an A/B testing configuration for two independent features.
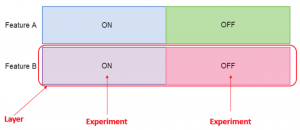
Now, it becomes clear when a user can participate in multiple experiments. Within each layer, a user can only be in one experiment but across layers, this constraint does not apply. Now we just need a way to assign users to an experiment within each layer.
Ensuring that traffic is always allocated fairly
When users are being assigned to multiple experiments, it is easy to allocate traffic (i.e. mapping users to expeirments) in a way that is unfair and leads to biased and unmeaningful results. Consider our two independent features scenario and imagine that users are distributed horizontally across the diagram:
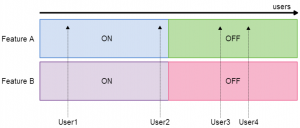
Here, we can see that if a user is assigned the experiment Feature A: On, they will also be assigned Feature B: On. So, if we later analyse the KPIs for the purple users vs the red users, we will have no idea whether any change in the KPIs has come from Feature A or Feature B. We need to allocate traffic in a fair way:
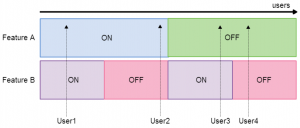
Here, the users assigned Feature A: On are equally split over Feature B: On and Feature B: Off. Now, if we look at the KPIs for the purple users vs the red users, we know that any change we see is purely down to Feature B. We have achieved this by partitioning experiments within each layer equally across experiments within the other layer.
In this simple example, where we only have two layers and two experiments within each layer, with a 50/50 traffic split, the partitioning solution is simple. However, our generic service needed to be able to handle scenarios where there are potentially many layers and many experiments within each layer, with arbitrary traffic splits. To solve this, we took another approach. Instead of ensuring experiments are partitioned fairly and then assigning a user to a fixed position across all layers, we randomly assign users to a position within each layer. To build the logic behind this, we introduce a new concept:
- Bucket – A layer is split into many buckets and a bucket maps to a single experiment. This is used in traffic allocation: a user is assigned a bucket and that bucket determines which experiment they land in.
As long as users are uniformly distributed across the buckets in each layer, and there is no dependence between the assignments in one layer and the assignments in another, then we will end up with a fair allocation but with much simpler logic than the experiment partitioning approach would require. We also must ensure that any given user is always assigned to the same bucket within each layer – we don’t want users to end up in different experiments in subsequent requests. Effectively, we need a random but deterministic mapping from users to buckets which is independent between layers.
To achieve this, we concatenate the user’s ID with each layer ID, and then use a hash function to map the user to a bucket within each layer:
|
1 2 3 4 5 |
for (layer : layers) { val bucket = Math.abs(hash(userId + layer.layerId)) % 1024; val experiment = getExperiment(layer, bucket); // use experiment to determine user experience } |
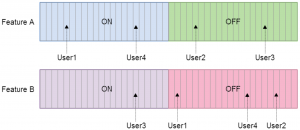
As long as we use a good hash function and choose a power of two for our number of buckets (see this stackoverflow post for an explanation), this will give the random but deterministic mapping that we need. For four users, we may end up with a mapping that looks something like this:
Configuring experiments with eligibility criteria
Another requirement for our A/B testing framework was to enable experiments to have some kind of eligibility criteria which cause the experiment to only be active under certain conditions. This means associating a set of attributes with the experiment. For example, the attributes {“country”: “UK”, “gender”: “male”} indicate that a user is only eligible for an experiment if they are male and live in the UK. If a user lands in an experiment that they are not eligible for, we give them the ‘default experience’, and to avoid introducing bias that user’s data is discarded and not considered when calculating KPIs.
When using the layer model and eligibility criteria are involved, there are situations where we can introduce new layers for the purpose of minimizing the amount of data discarded. For example, say that we want to test Feature A only in the UK and Denmark. We could define a layer with four experiments, like this:

This works and adheres to our original definition of a layer, however this configuration results in some traffic being discarded unnecessarily. For example, if a UK user lands in a Denmark experiment, they will be given the default experience but will not participate in an experiment. This is clearly not optimal – only 50% of UK and DK users will participate in an A/B test. To avoid this wastage, we can simply use two layers instead of one:

Defining multiple layers in this way is acceptable whenever the users eligible for each experiment are disjoint. If this was not the case in the above example, then we may end up with a conflict: a user could be assigned ON in one layer and OFF in another. If we wanted to add another A/B test, testing Feature A on all male users, then we would have to define all experiments in a single layer as there is some overlap in eligible users.
As we’ve seen, A/B testing can become fairly complex when running multiple simultaneous experiments and there are some subtle issues that must be addressed in order to ensure that experiments are fair, meaningful and optimally allocated to minimise wasting valuable traffic. For a tech company, A/B testing has enough complexity to warrant building it as an isolated service, enabling you to have powerful A/B testing functionality across a range of applications without needing to deal with the same problems in multiple projects.